CSS Trigonometric Functions

You already know of min(), max() and calc(). But did you know that as of December 2022,  Firefox and Safari began supporting CSS trigonometric functions. Later on other browsers would follow suit.

But Why Another Mathematical Complexity?

From our research and personal tries, the main reason seems to be to create complex animations without needing so much JavaScript. But let us first find out what these trigonometric functions are.

The basic CSS trigonometric functions are:  sin(), cos(), tan(), asin(), acos(), atan(), and atan2(). These functions are defined in the CSS Values and Units Module Level 4 and are now supported by all browsers.

sin(), cos(), and tan()

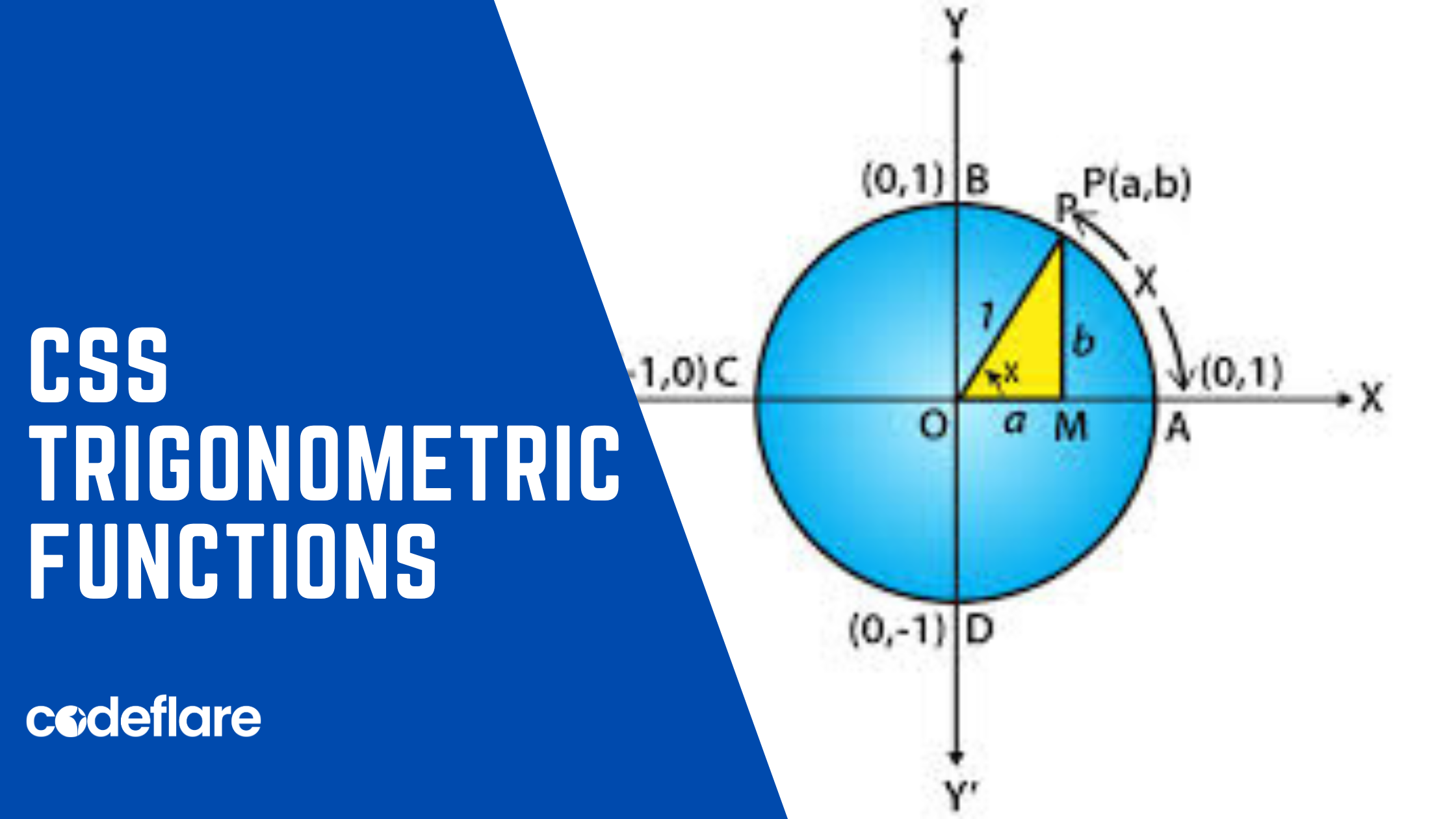
The core three trig functions are:

• cos(): Returns the cosine of an angle, which is a value between -1 and 1.
• sin(): Returns the sine of an angle, which is a value between -1 and 1.
• tan(): Returns the tangent of an angle, which is a value between −∞ and +∞.

Unlike their JavaScript counterparts, these functions accept both angles and radians as their argument. Let’s see some syntax:

cos()

/* Single <angle> values */
width: calc(100px * cos(45deg));
width: calc(100px * cos(0.125turn));
width: calc(100px * cos(0.785398163rad));

/* Single <number> values */
width: calc(100px * cos(63.673));
width: calc(100px * cos(2 * 0.125));

/* Other values */
width: calc(100px * cos(pi));
width: calc(100px * cos(e / 2));

sin()

/* Single <angle> values */
width: calc(100px * sin(45deg));
width: calc(100px * sin(0.25turn));
width: calc(100px * sin(1.0471967rad));

/* Single <number> values */
width: calc(100px * sin(63.673));
width: calc(100px * sin(2 * 0.125));

/* Other values */
width: calc(100px * sin(pi / 2));
width: calc(100px * sin(e / 4));

tan()

/* Single <angle> values */
width: calc(100px * tan(45deg));
width: calc(100px * tan(0.125turn));
width: calc(100px * tan(0.785398163rad));

/* Single <number> values */
width: calc(100px * tan(0.5773502));
width: calc(100px * tan(1.732 - 1));

/* Other values */
width: calc(100px * tan(pi / 3));
width: calc(100px * tan(e));

Real-life Use Cases

There are several use cases for CSS trigonometric functions. In the following example, the dots revolve around a central point. Instead of rotating each dot around its own center and then moving it outwards, each dot is translated on the X and Y axes. The distances on the X and Y axes are determined by taking the cos() and, respectively, the sin() of the --angle into account.

To distribute the dots evenly around the central point, each dot is given an additional offset based on its nth-childindex. For example, if there are three dots, there’s a distance of 120deg (= 360deg / 3) between each dot.

• The first child element out of three gets offset by 0 x 120deg = 0deg.
• The second child element out of three gets offset by 1 x 120deg = 120deg.
• The third child element out of three gets offset by 2 x 120deg = 240deg.

Summary

If you’re just building simple websites you may have little or no encounters with CSS trigonometric functions. The primary use case for these seems to be easier shape creation and more options for building complex animations.

Differences between Functional and Class Components

codeflare